1-POTENCIA DE
NÚMEROS NATURALES
La
potencia es una nueva operación matemática que aparece en la escuela
secundaria, pero esto no significa que sea difícil o algo totalmente nuevo.
Veamos qué significa potenciar un número.
Potenciar un número significa multiplicarlo varias veces por
él mismo, es decir, si quiero potenciar el 5 por ejemplo 3 veces, entonces
tengo que multiplicarlo 3 veces, o sea multiplicar 3 veces el 5:
\[5\times 5\times 5=125\]
De esta manera, podemos decir que potenciar un número es
multiplicar ese número una cierta cantidad de veces repetidas. Si pensamos
bien, esto es una cosa fácil de hacer. Ahora la pregunta que se nos viene a la
mente es ¿cómo escribimos una potencia en forma matemática? Por ejemplo, no
está bueno escribir “potenciar 3 veces el 5”, debe haber una forma más corta de
escribir esta operación matemática. Los matemáticos resuelven de manera muy
fácil las cosas de escritura y “potenciar 3 veces el 5” lo escriben de esta
manera:
\[5^3\]
El número que se encuentra arriba nos dice la cantidad de veces
que debemos multiplicar (potenciar) el número de abajo. Entonces, cada vez que
queramos potenciar un número, simplemente escribimos el número que queremos
potenciar y le colocamos la cantidad de veces que lo queremos multiplicar con
un numerito un poco más arriba.
Si pensamos un poco, vemos que la potencia no es otra cosa que
multiplicar repetidamente un mismo número. Miremos el siguiente ejemplo y
encontremos su potencia: “potenciar 6 veces el 2”, esto significa multiplicar 6
veces el 2 y se escribe de manera resumida así:
\[2^6\]
Si resolvemos esta potencia, quedaría:
\[2^6=2\times 2\times 2\times 2\times 2\times 2=64\]
Recordemos que cuando hay muchas multiplicaciones por resolver,
vamos resolviendo de a dos números por vez, o sea $2\times 2\times 2\times 2\times 2\times 2=4\times 4\times 4=64$.
Entonces ahora que sabemos qué es una potencia, pasemos al
concepto matemático.
Concepto: La potencia es una operación matemática entre dos números, uno llamado base y el otro llamado exponente. El exponente nos dice cuántas veces debemos multiplicar la base (esto lo llamamos potenciar la base).
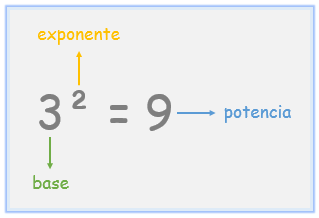
En el ejemplo $2^6$, la base es el 2 y el exponente es el 6.
Una cosa importante que hay que notar es que $2^6$ no significa que tengo
que multiplicar el 2 con el 6, sino que significa que tenemos que multiplicar 6
veces el 2, no es lo mismo.
También podemos decir que la potencia sirve para escribir de
manera más resumida aquellas multiplicaciones en las que se repiten varias
veces el mismo número. Por ejemplo, si tenemos el siguiente cálculo
\[3\times 3\times 3\times 3\times 3\times 3\times 3\times 3\times 3 + 2\times 2\times 2\times 2\times 2\]
En lugar de escribirlo
así, como una "super" multiplicación, podemos usar las potencias para que quede
más resumido, miremos que se puede usar potencia porque en los dos casos tenemos
una base que se repite, el 3 se repite 9 veces en el primer término y el 2 se
repite 5 veces en el segundo término. Entonces este cálculo se podría escribir
así:
\[3^9+2^5\]
¿Queda mejor no?
Ahora, miremos qué pasa si queremos potenciar solo una vez un
número. Por ejemplo, te piden potenciar 1 vez el 12. Esto sería escrito de esta
manera
\[12^1\]
Pero si nos damos cuenta, en este caso el exponente es 1, o sea
que tenemos que multiplicar una vez el 12, entonces no lo vamos a potenciar en
realidad, porque es un solo 12, por lo tanto nos queda lo mismo, o sea:
\[12^1=12\]
Por último, vamos ver como se lee una potencia (recordar cuál es
la base y cual es el exponente). Los exponentes se leen como números de orden
(primera, segunda, tercera, cuarta, etc.). Entonces, una potencia se lee “la
base a la exponente”. Por ejemplo, leemos las siguientes potencias:
$23^5$ se lee "veintitrés a la quinta".
$1^7$ se lee "uno a la séptima".
$2^4$ se lee "dos a la cuarta".
Ahora, cuando el exponente es un 2, no se suele usar “a la
segunda” sino “al cuadrado”. Por ejemplo:
$4^2$ es "cuatro al cuadrado".
$6^2$ es "seis al cuadrado".
Y cuando el exponente es un 3, no se suele leer “a la tercera”
sino “al cubo”. Por ejemplo:
$2^3$ es "dos al cubo".
$5^3$ es "cinco al cubo".
2-RADICACIÓN EN NÚMEROS NATURALES
Una vez que hemos entendido la
operación matemática de potenciar, podemos realizar la pregunta sobre el número
que debemos potenciar para obtener un determinado resultado. Por ejemplo,
podríamos preguntar ¿qué número debemos potenciar dos veces para obtener 9 de
resultado? Entonces, pensemos en la pregunta, nos habla de potenciar dos veces,
sabemos que eso significa multiplicar dos veces un mismo número. De esta
manera, la pregunta se reduce a encontrar un número que cuando lo
multipliquemos dos veces, nos dé 9 de resultado; es decir:
\[\square^2=\square\times\square=9\]
Debemos encontrar el
número que deberíamos colocar en el cuadradito, es importante que darse cuenta
que no podemos poner números diferentes, debe ser el mismo número multiplicado
dos veces porque potenciar significa justamente eso.
Entonces, si no se nos
ocurre algún número, debemos ir probando y ver cual cumple con lo que pedimos:
$1^2=1\times 1=1$ (no da 9, entonces el 1 no es la respuesta).
$2^2=2\times 2=4$ (no da 9, entonces el 2 no es la respuesta).
$3^2=3\times 3=9$ (el 3 es la respuesta).
Entonces, probando
número, encontramos la respuesta: el 3 es el número que debemos potenciar dos
veces para obtener 9 de resultado. Ahora, no está bueno tener que escribir una
pregunta muy larga cada vez que queremos averiguar un resultado, entonces viene
la escritura en forma matemática. La pregunta ¿qué número debemos
potenciar dos veces para obtener 9 de resultado? se escribe matemáticamente
así:
Esto es mucho mejor que
escribir una pregunta larga. Ahora, la respuesta a esa pregunta es el 3 como lo
habíamos visto, entonces escribimos:
\[\sqrt[2]{9}=3\]
Miremos otro ejemplo un
poco más difícil:
\[\sqrt[2]{49}\]
Esto nos pregunta ¿qué
número debemos potenciar 2 (dos) veces para que tengamos 49 de resultado?; para
contestar esto debemos buscar ese número. Si no se nos ocurre la respuesta,
debemos probar potenciando 2(dos) veces los números hasta ver cuál nos da 49 de
resultado:
$1^2=1\times 1=1$ (no es el 1 porque no da 49).
$2^2=2\times 2=4$ (no es el 2 porque no da 49).
$3^2=3\times 3=9$ (no es el 3 porque no da 49).
$4^2=4\times 4=16$ (no es el 4 porque no da 49).
$5^2=5\times 5=25$ (no es el 5 porque no da 49).
$6^2=6\times 6=36$ (no es el 6 porque no da 49).
$7^2=7\times 7=49$ (entonce el 7 es la respuesta porque $7^2=49$).
Entonces tenemos la
respuesta a la pregunta:
\[\sqrt[2]{49}=7\]
Conclusión: la
operación matemática que estamos realizando a través de las preguntas
anteriores se llama “raíz cuadrada”. Se llama raíz cuadrada porque estamos
pensando en potencias cuadradas.
De esta manera, podemos
realizar preguntas parecidas a la anterior: ¿qué número debemos potenciar 3
(tres) veces para obtener 64 de resultado? En este caso, debemos buscar el
número que multiplicado 3 veces nos de 64 de resultado, o sea buscar qué número
debemos colocar el en cuadradito:
\[\square^3=\square\times \square\times \square=64\]
En principio, si no se
nos ocurre, debemos buscar el número probando:
$1^3=1\times 1\times 1=1$ (no es el 1 porque no da 49).
$2^3=2\times 2\times 2=8$ (no es el 2 porque no da 49).
$3^3=3\times 3\times 3=27$ (no es el 3 porque no da 49).
$4^3=4\times 4\times 4=64$ (la respuesta es el 4, porque $4^3=64$).
Entonces la respuesta
de nuestra pregunta es el 4, y si escribimos matemáticamente la pregunta con su
respuesta, quedaría así:
Conclusión:
Esta operación matemática que estamos realizando se llama “raíz cubica” porque
estamos pensando en número potenciados al cubo.
Ahora vamos a ver el
concepto de radicación como una nueva operación matemática.
CONCEPTO:
la radicación es una operación matemática entre dos números, uno llamado índice
y otro llamado radicando.
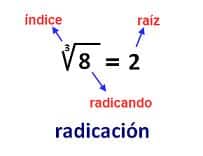
La raíz es aquel número que potenciado la
cantidad de veces que indica el índice, da el radicando. Es decir, la raíz es
la respuesta a la pregunta que plantea la radicación.
En el ejemplo, la
pregunta es ¿Cuál es el número que potenciado tres veces, da 8? Tal número es
el 2.
La radicación se lee de la misma manera
que en las potencias:
$\sqrt[2]{25}$ se lee "raíz cuadrada de veinticinco".
$\sqrt[3]{64}$ se lee "raíz cúbica de sesenta y cuatro".
$\sqrt[4]{81}$ se lee "raíz cuarta de ochenta y uno";
y así sucesivamente. Miremos cual es el
resultado de las raíces anteriores:
$\sqrt[2]{25}=5$
$\sqrt[3]{64}=4$
$\sqrt[4]{81}=3$



No hay comentarios.:
Publicar un comentario